二叉树的定义
二叉树是树形结构的一个重要类型，许多实际问题抽象出来的数据结构往往是二叉树的形式，即使是一般的树也能简单的转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得尤为重要。二叉树的特点是每个节点最多只能有两棵子树，且有左右之分。
二叉树是有n个有限元素的集合，该集合或者为空，或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树，当集合为空时，称该二叉树为空二叉树，在二叉树中，一个元素也称为一个节点。
下图为树的示意图
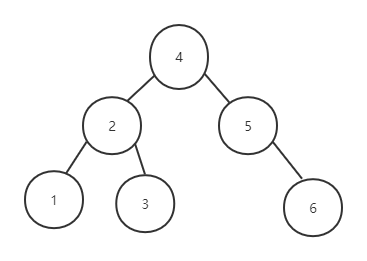
图表 1
二叉搜索树（又称二叉排序树、二叉查找树），它或者是一颗空树，又或者是具有如下性质的二叉树：
1.若它的左子树不为空，则左子树所有节点的值小于根节点；
2.若它的右子树不为空，则根节点小于所有的右子树结点的值；
3.它的左右子树叶分别为二叉排序树。
根据节点的值排序就是：左子树<根节点<右子树
中序遍历一颗二叉树可以得到一个结点值递增的有序序列。
如下图二叉树：
图表 2
它的中序遍历是：1、2、3、4、5、6，正好就是排好序的。
二叉搜索树是能够高效地进行如下操作的数据结构。
1.插入一个数值
2.查询是否包含某个数值
3.删除某个数值
本文章整理二叉搜索树的查找。
在二叉排序树中查找目标元素，就是从树根节点出发，先将树根节点和目标元素作比较：
若该节点不存在，则查找失败；若当前节点的值和目标值相等，则查找成功
若当前节点的值比目标值小，那么目标值只可能位于当前节点的左子树中，所以下一步继续进入左子树查找
若当前节点的值比目标值大，那么目标值只可能位于当前节点的右子树中，所以下一步继续进入右子树查找。
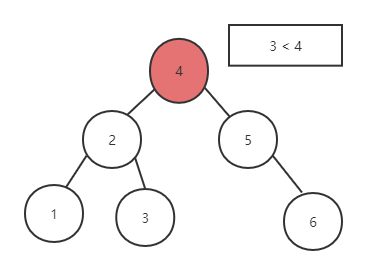
以图表2的二叉排序树为例，查找元素3的过程是：
从树根节点出发，4比目标值3大，则3只可能位于4的左子树中，继续进入左子树查找
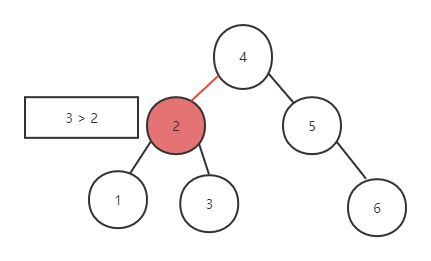
当前子树根节点的值为2，2比3小，则3只可能位于2的右子树，继续进入右子树查找
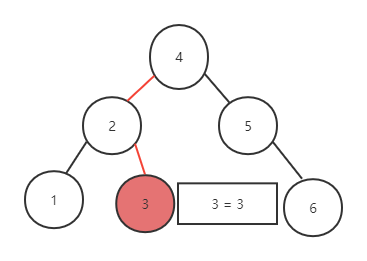
当前子树根节点的值为3，和目标值相等，则查找成功
编码实现二叉排序树中查找目标元素，代码如下：
struct tree_node *find(struct tree_node *tree, int num)
{
if(tree == NULL) {//如果当前节点为NULL 则返回NULL
return NULL;
}
if(num == tree->num) { //如果查找成功 则返回目标值
return tree;
}
if(num > tree->num) {//如果目标值大于当前节点的值，则继续在右子树查找
return find(tree->rch, num);
}
if(num < tree->num) {//如果目标值小于当前节点的值，则继续在左子树查找
return find(tree->lch, num);
}
}
3279916262