二叉树创建：
二叉树一般手动创建并连接每一个节点，此处创建的是有序二叉树。
struct tree
{
int data;
struct tree *left, *right;
};
void createTree( struct tree **tree, struct tree *newNode )
{
if( *tree == NULL )
{
*tree = newNode;
return;
}
if( (*tree)->data > newNode->data )
{
createTree( (&(*tree)->left), newNode );
}
else
{
createTree( (&(*tree)->right), newNode );
}
}
void initTree( struct tree **root, int *parr, int len )
{
int i = 0;
for( i=0; i<len; i++ )
{
struct tree *node = malloc( sizeof(struct tree) );
node->data = *(parr + i);
node->left = NULL;
node->right = NULL;
createTree( root, node );
}
}
二叉树遍历：
前中后序遍历：
这三种遍历都是深度优先。遵循的顺序如下：
前序遍历——访问根结点的操作发生在遍历其左右子树之前。
中序遍历——访问根结点的操作发生在遍历其左右子树之中。
后序遍历——访问根结点的操作发生在遍历其左右子树之后。
前序遍历：
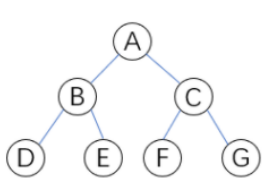
前序遍历可理解为“延外圈遍历所有节点”，逻辑为：先根、再左、再右。如图按照前序遍历时，结果为：A、B、D、E、C、F、G。
// 先根、再左、再右
void preorder( struct tree *tree )
{
if( tree == NULL )
{
return;
}
printf( "tree = %d ", tree->data );
preorder( tree->left );
preorder( tree->right );
}
中序遍历：
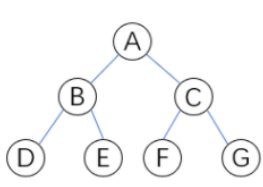
中序遍历可理解为“从左往右，从上往下遍历所有节点”，逻辑为：先左、再根、再右。如图按照前序遍历时，结果为：D、B、E、A、F、C、G。
// 先左、再根、再右
void inorder( struct tree *tree )
{
if( tree == NULL )
{
return;
}
inorder( tree->left );
printf( "tree = %d ", tree->data );
inorder( tree->right );
}
后序遍历：
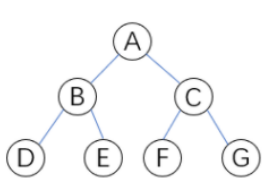
后序遍历可理解为“从左边第一个叶子节点开始向上一级一级遍历所有节点（往后面遍历时，优先找到最下层的叶子节点）”，逻辑为：先左、再右、再根。如图按照前序遍历时，结果为：D、E、B、F、G、C、A。
// 先左、再右、再根
void postorder( struct tree *tree )
{
if( tree == NULL )
{
return;
}
postorder( tree->left );
postorder( tree->right );
printf( "tree = %d ", tree->data );
}
完整代码：
#include <stdio.h>
#include <stdlib.h>
struct tree{
int data; // 数据域
struct tree *left； // 左子树
struct tree *right； // 右子树
};
// 创建二叉树
void createTree( struct tree **tree, struct tree *newNode )
{
if( *tree == NULL )
{
*tree = newNode;
return;
}
if( (*tree)->data > newNode->data )
{
createTree( (&(*tree)->left), newNode );
}
else
{
createTree( (&(*tree)->right), newNode );
}
}
void initTree( struct tree **root, int *parr, int len )
{
int i = 0;
for( i=0; i<len; i++ )
{
struct tree *node = malloc( sizeof(struct tree) );
node->data = *(parr + i);
node->left = NULL;
node->right = NULL;
createTree( root, node );
}
}
// 前序遍历
void preorder( struct tree *tree )
{
if( tree == NULL )
{
return;
}
printf( "tree = %d ", tree->data );
preorder( tree->left );
preorder( tree->right );
}
// 中序遍历
void inorder( struct tree *tree )
{
if( tree == NULL )
{
return;
}
inorder( tree->left );
printf( "tree = %d ", tree->data );
inorder( tree->right );
}
// 后序遍历
void postorder( struct tree *tree )
{
if( tree == NULL )
{
return;
}
postorder( tree->left );
postorder( tree->right );
printf( "tree = %d ", tree->data );
}
int main()
{
int arr[] = {1,2,3,4,5,6,7,8,9};
int len = sizeof(arr)/sizeof(arr[0]);
struct tree *root = NULL;
initTree( &root, arr, len );
preorder( root );
//inorder( root );
//postorder( root );
return 0;
}
3279916262